KAHOOT Teorema de Euler
Objetivo
Desarrollar
una evaluación interactiva que permita reforzar los contenidos revisados sobre
el contenido teórico práctico de Euler.
Contenido
- Datos biográficos
- Fórmula de Euler
- Importancia en la construcción de poliedros
- Aplicaciones a la teoría de grafos.
Se aplica una evaluación dinámica en el
laboratorio de informática para reforzar los contenidos más relevantes descritos
en la clase de Teorema de Euler.
Recursos
- Plataforma Kahoo
- Códigos
- Computadores
- Conexión a internet
Evaluación
Sobre 5 puntos
7 min
TRIÁNGULO DE PASCAL E-ACTIVIDAD MEJORADA
| 1.Objetivo de aprendizaje | ||
| Analizar las propiedades del triángulo de Pascal, utilizando como punto de partida el binomio de la forma |
||
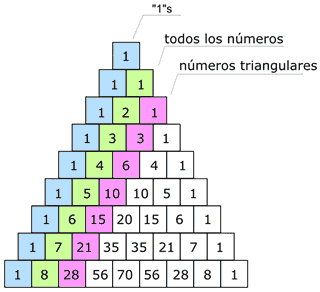
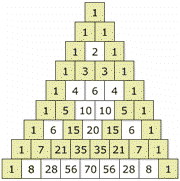
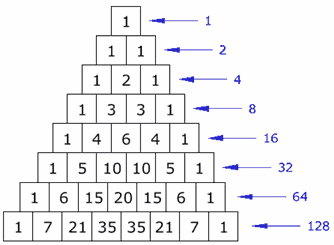
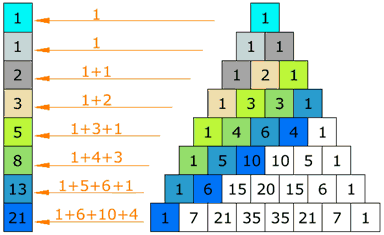
| 2. Contenidos que aborda la e-actividad Una de las pautas de números más interesantes él es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés). |
||
| 3. Descripción de la e-actividad | ||
Se modelará ecuaciones matemáticas en el software Geogebra que respondan a las propiedades del Triángulo de Pascal de tal manera que en un máximo de 4 ecuaciones se describan las 10 propiedades de una manera gráfica y visible. Además se considera el estudio de las características básicas y funciones del software Geogebra que permita graficar los modelos matemáticos mencionados. |
||
Para describir la actividad a continuación se desarrollará los aspectos a trabajar de manera específica: · Ingresar al link de recursos y descargar los documentos a estudiar. · Realizar un análisis grupal acerca de las propiedades del triángulo de Pascal · Debatir cuales de las propiedades son más visibles en la naturaleza · Elaborar modelos matemáticos de las propiedades principales · En el software Geogebra ingresar los modelos matemáticos elaborados · Analizar las gráficas elaborados, hallar diferencias y semejanzas · Diseñar una infografía con las gráficas, semejanzas y diferencias halladas. · Compartir la infografía a través de redes sociales. |
||
| Tarea 1: Infografía sobre propiedades del Triángulo de Pascal | ||
| Foro 1: Utilidad de las propiedades del Triángulo de Pascal | ||
Tarea 2: Para realizar una aplicación del triángulo de Pascal y sus propiedades; deberás seguir los siguientes pasos: 1.- Reunirse en equipos de 3 o 4 personas y buscar en Internet páginas o vídeos de donde puedan obtener información para ampliar más el tema del triángulo de Pascal. 2. Con la información obtenida, realizar un vídeo donde se expliquen cada uno de los problemas; explicando la fórmula matemática, elementos, características, diseño en Geogebra. DATOS QUE DEBE CONTENER EL VÍDEO: · Título del Tema · Nombre del docente · Nombres de los integrantes del equipo · Grupo · Fecha 3. El objetivo de demostrar o comprobar las propiedades del Triángulo de Pascal mientras se graban en vídeo. 4. Finalmente deben generar una conclusión contestando a la pregunta: ¿Para qué me sirve el Triángulo de Pascal? 5. Deben enviar el URL (link) de sus videos al correo del docente: matematikinteractiva_carlos@hotmail.com |
||
Tarea 3: Aplicación realizada en Geogebra Compruebe en geogebra las siguientes propiedades: · Números poligonales · El "stick de hockey" Nota: Las tareas tendrán una calificación sobre 10, utilizando una rúbrica. Foros: Idóneo o no idóneo. |
||
Tarea 4: Ingresar al ThatQuiz del siguiente link: https://www.thatquiz.org/es/practicetest?iy3qiojzc493 En este link se puede evaluar el contenido que refiere analizar las propiedades del triángulo de Pascal mediante la resolución de problemas. Como herramienta didáctica adicional tenemos a Geogebra que es un programa dinámico para la Enseñanza y Aprendizaje de las matemáticas para educación en todos sus niveles. Combina dinámicamente, geometría, álgebra , análisis y estadística en un único conjunto tan sencillo a nivel operativo. Este programa les facilitara la evaluación ya que permite abordar la geometría desde una forma dinámica e interactiva que ayuda a los estudiantes a visualizar contenidos matemáticos que son más complicados de afrontar desde un dibujo estático. También permite realizar construcciones de manera fácil y rápida, con un trazado exacto y real, que además, revelarán las relaciones existentes entre la figura construida; también permitirá la transformación dinámica de los objetos que la componen. Debido a estas dos características el profesorado y el alumnado pueden acercarse a GeoGebra de varias maneras, no excluyentes entre sí pero que a menudo están relacionadas con el nivel de capacitación que se tenga del programa. |
||
| 4. Recursos | ||
Recursos Materiales
|
- Cuaderno de la materia de matemática - Lápiz - Bolígrafos colores “Rojo” y “Azul” - Regla |
|
Recursos de lectura |
https://www.uaeh.edu.mx/docencia/P_Presentaciones/prepa2/2018/Proyecto_de_Algebra.pdf | |
Recursos visuales |
https://www.youtube.com/watch?v=DPxIbJ-Rbf4 | |
| Recursos informáticos | - Computador - Software Matemático Geogebra - Carpeta Drive documentos y software https://drive.google.com/drive/folders/1uBY8PLixYHHRiy__-onjUGivNIBcWfIX?usp=sharing |
|
| Temporalización |
Las e-actividades planteadas se realizarán en el transcurso de la semana del 11 al 20 de diciembre. | |
| Evaluación |
|
|
E-ACTIVIDAD EULER
|
Componente
|
Descripción
|
|
Etapa
|
Acceso y
motivación
|
|
Nombre de la
actividad
|
Cuestionario en
la plataforma Kahoot
|
|
Propósito
|
Desarrollar una
evaluación interactiva que permita reforzar los contenidos revisados sobre el
contenido teórico práctico de Euler.
|
|
Chispa
|
Construyamos un
tetraedro en 3 minutos papel periódico o de revista.
Lectura en casa
de La Historia de los números.
|
|
Número de
participantes
|
28
|
|
Estructura
|
Resolución de
cuestionario en la plataforma Kahoot.
Determinar de
ganadores por la rapidez en la resolución.
Determinar
ganadores por aciertos.
|
|
Acciones de los
estudiantes
|
Ingreso de
código de inicio.
Socialización de
resultados en el laboratorio de informática.
|
|
Tiempo de los
estudiantes
|
120 minutos.
|
|
Normas
|
Lectura previa
de la historia de los números se revisará el subrayado.
Construcción de
un tetraedro se revisará las fotografías.
Participar en el
aula con la resolución del cuestionario.
|
|
Acciones del
docente
|
Se aplica una
evaluación dinámica en el laboratorio de informática para reforzar los
contenidos más relevantes descritos en la clase de Teorema de Euler.
|
|
Tiempo del
docente
|
40 minutos.
|
|
Evaluación y
resultados esperados
|
Cuestionario.
Estudiantes en un
80% motivados para la aplicación práctica del teorema de Euler en los
ejercicios de cálculo de aristas, vértices y caras.
|
|
Herramientas
tecnológicas
|
Plataforma Kahoo
Enlace https://create.kahoot.it/creator/925136ad-00ea-4d07-ad42-eaf9d3552fc5
|
|
Vínculo con
otras actividades
|
Ampliemos de
manera interesante este tema con el video Doblando papel.
|