E-Actividad Zwick/Roell
Definición de los objetivos o competencias específicos a alcanzar.
- Conocer qué son y cuál es la finalidad de la Actividades de formación.
- Comprender las actividades como elemento de un proceso formativo.
- Conocer los diversos significados didácticos de las actividades.
- Adquirir las capacidades necesarias para seleccionar, crear o
- diseñar actividades de formación.
Descripción del contenido que aborda la actividad.
Esta actividad está dirigida a docentes en formación y explicara de una manera directa la
Teleformación la cual exige que nos esforcemos en conseguir que ésta no se convierta
únicamente en un medio más de entrada y acceso a la información. Si lo que pretendemos
es evitar que los entornos de formación se conviertan en entornos simplemente expositivos
y de almacenamiento de la información, ante los cuales el alumno únicamente debe
acceder a ella y memorizarla, se deben incluir una serie de recursos que faciliten desde la
comprensión de los contenidos, hasta la profundización en los mismos.
Probablemente una de las formas que tenemos para no caer en lo anteriormente expuesto,
pasa por la incorporación de diferentes actividades que persigan:
-La deflexión del estudiante sobre los contenidos.
-El establecimiento de una estructura más dinámica para la interacción del propio sujeto
con la información presentada.
Estimación del tiempo que el estudiante dedicará a la actividad.
Para esta actividad el estudiante tendrá 5 días que irán comprendidos y distribuidos de la
siguiente manera
Del lunes 17/02/2020 al martes 18/02/2020 presentación del primer borrador
Miércoles 19/02/2020 presentación del segundo borrador
Jueves 20/02/2020 presentación final del ensayo
Viernes 21/02/2020 exposición y defensa del ensayo ante sus compañeros y docente
Selección y disposición de los recursos TIC.
Biblioteca institucional con acceso libre a computadores e internet de fibra óptica
Cibercafés institucionales con acceso libre de wifi
Recursos Tics
Uso institucional libre con activación de licencia Premium del software de edición Zwick/Roell
Explicación de los criterios de evaluación
El ensayo será calificado bajo los estándares de la siguiente rubrica de evaluación
Complementos importantes:
1) Falto bibliografía: 25% menos, se considera plagio
2) Presencia de copy-paste: Si hay más de 2 párrafos con copy-paste o más de uno
igual a la de algún compañero obtendrá 1/10 de calificación.
3) Ortografía: cada error dará un 1% menos. (Tolerancia 1 por página)
4) Descuidos de escritura: cada error dará un 1% menos. (Tolerancia 1 por página)
Orientaciones para que otros docentes puedan aplicar la idea que propone esta e-
actividad.
- Se recomienda brindar una retroalimentación adecuada independientemente a cada estudiante según el enfoque que han decidido analizar
- Brindar concejos y recomendaciones de cómo se debe realizar ensayos adecuados mediante documentación y herramientas digitales
- Proporcionar al estudiante tiempos de corrección y coevaluación en la presentación de sus borradores
E-Actividad GEOGEBRA
Etapa: Investigación, Desarrollo y aplicación
Nombre de la actividad: Conociendo los principios de aplicación del triángulo de pascal
Propósito: Que el estudiante analice las propiedades del triángulo de Pascal, utilizando
como punto de partida el binomio de la forma formula conocido con el Binomio
de Newton, al ser la propiedad más visible del triángulo hasta encontrar las 10 propiedades
y describirlas gráficamente a través del uso del software libre geogebra
Chispa: “Dios creo las matemáticas en la creación del mundo y de todos sus habitantes”
Número de estudiantes: Grupo de 5 estudiantes
Estructura:
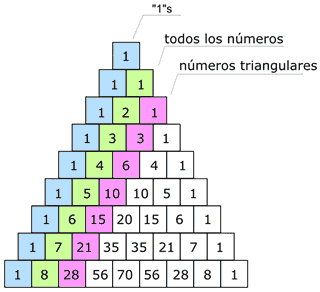
TRIÁNGULO DE PASCAL
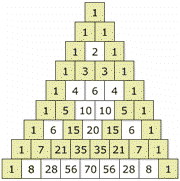
Una de las pautas de números más interesantes el es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés). Para construir el triángulo, empieza con "1" arriba, y pon números debajo formando un triángulo. Cada número es la suma de los dos números que tiene encima, menos los extremos, que son siempre "1". (Aquí está remarcado que 1+3 = 4)
DETALLES DEL TRIÁNGULO DE PASCAL
Pares e impares
Si usas distintos colores para los números pares e impares,
obtienes un patrón igual al del Triángulo de Sierpinski
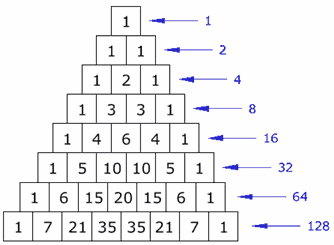
Sumas horizontales
¿Notas algo en las sumas horizontales? ¿Hay algún patrón? ¡Es increíble! Se dobla cada vez (son las potencias de 2)
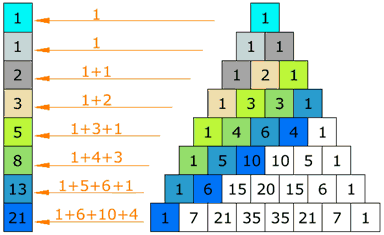
Sucesión de Fibonacci
Prueba esto: empieza con un 1 de la izquierda, da un paso arriba y uno al lado, suma los cuadrados donde caigas (como en el dibujo)... las sumas que salen son la sucesión de Fibonacci.
(La sucesión de Fibonacci se hace sumando dos números para conseguir el siguiente, por ejemplo 3+5=8, después 5+8=13, etc.)
(La sucesión de Fibonacci se hace sumando dos números para conseguir el siguiente, por ejemplo 3+5=8, después 5+8=13, etc.)
Acciones de los estudiantes:
Para describir la actividad a continuación se desarrollará los aspectos a trabajar de manera específica:
- Ingresar al link de recursos y descargar los documentos a estudiar.
- Realizar un análisis grupal acerca de las propiedades del triángulo de Pascal
- Debatir cuales de las propiedades son más visibles en la naturaleza
- Elaborar modelos matemáticos de las propiedades principales
- En el software Geogebra ingresar los modelos matemáticos elaborados
- Analizar las gráficas elaborados, hallar diferencias y semejanzas
- Diseñar una infografía con las gráficas, semejanzas y diferencias halladas.
- Compartir la infografía a través de redes sociales.
- Con la información obtenida, realizar un vídeo donde se expliquen cada uno de los problemas; explicando la fórmula matemática, elementos, características, diseño en Geogebra.
DATOS QUE DEBE CONTENER EL VÍDEO:
- Título del Tema
- Nombre del docente
- Nombres de los integrantes del equipo
- Grupo
- Fecha
- Tiempo de los estudiantes:
Las e-actividades planteadas se realizarán en el transcurso de la semana del 11 al 20 de febrero
Normas:
Todas las actividades propuestas deben presentarse en el tiempo establecido no se
aceptaran actividades fuera de este tiempo
Actividades replicadas de otros grupos serán penalizadas con la calificación de 1/10
Todos los documentos presentados deben tener el formato institucional establecido
para la presentación de proyectos
Acciones del docente:
- El docente receptara los trabajos grupales hasta la fecha establecida
- El docente aceptara borradores o consultas de los estudiantes que así lo requieran antes de la fecha de entrega y realizara una retroalimentación de ser necesario
- Tiempo del docente
- El docente iniciara la calificación de los trabajos grupales a partir del 21 de febrero hasta el 27 del mismo mes,
- Las calificaciones obtenidas por los estudiantes serán publicadas a partir del 28 de febrero mediante la plataforma institucional
Evaluación y resultados esperado
El objetivo de demostrar o comprobar las propiedades del Triángulo de Pascal mientras se graban en vídeo.
Finalmente deben generar una conclusión contestando a la pregunta: ¿Para qué me sirve el Triángulo de Pascal?
Deben enviar el URL (link) de sus videos al correo del docente: matematikinteractiva_carlos@hotmail.com
1. Objetivo de aprendizaje
Analizar las propiedades del triángulo de Pascal, utilizando como punto de partida la forma conocido con el Binomio de Newton, al ser la propiedad más visible del triángulo hasta encontrar las 10 propiedades y describirlas gráficamente a través del uso del software libre geogebra, para demostrar la utilidad y aplicación del triangulo de pascal
2. Contenidos que aborda la e-actividad
Una de las pautas de números más interesantes él es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés).
En los contenidos a desarrollar se analizará:
Se modelará ecuaciones matemáticas en el software Geogebra que respondan a las propiedades del Triángulo de Pascal de tal manera que en un máximo de 4 ecuaciones se describan las 10 propiedades de una manera gráfica y visible.
Además se considera el estudio de las características básicas y funciones del software Geogebra que permita graficar los modelos matemáticos mencionados.
3. Descripción de la e-actividad
Para describir la actividad a continuación se desarrollará los aspectos a trabajar de manera específica:
E-ACTVIDAD MEJORADA
1. Objetivo de aprendizaje
Analizar las propiedades del triángulo de Pascal, utilizando como punto de partida la forma conocido con el Binomio de Newton, al ser la propiedad más visible del triángulo hasta encontrar las 10 propiedades y describirlas gráficamente a través del uso del software libre geogebra, para demostrar la utilidad y aplicación del triangulo de pascal
2. Contenidos que aborda la e-actividad
Una de las pautas de números más interesantes él es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés).
En los contenidos a desarrollar se analizará:
- Binomio de Newton
- Números poligonales
- Números triangulares
- Números cuadrados
- Números primos
- Suma de los elementos
- Sucesión de Fibonacci
- Potencias de 11
- El "stick de hockey"
- El triángulo de Sierpinski
Se modelará ecuaciones matemáticas en el software Geogebra que respondan a las propiedades del Triángulo de Pascal de tal manera que en un máximo de 4 ecuaciones se describan las 10 propiedades de una manera gráfica y visible.
Además se considera el estudio de las características básicas y funciones del software Geogebra que permita graficar los modelos matemáticos mencionados.
3. Descripción de la e-actividad
Para describir la actividad a continuación se desarrollará los aspectos a trabajar de manera específica:
- Ingresar al link de recursos y descargar los documentos a estudiar.
- Realizar un análisis grupal acerca de las propiedades del triángulo de Pascal
- Debatir cuales de las propiedades son más visibles en la naturaleza
- Elaborar modelos matemáticos de las propiedades principales
- En el software Geogebra ingresar los modelos matemáticos elaborados
- Analizar las gráficas elaborados, hallar diferencias y semejanzas
- Diseñar una infografía con las gráficas, semejanzas y diferencias halladas.
- Compartir la infografía a través de redes sociales.
4. Recursos y materiales necesarios
- Recursos Materiales
- Cuaderno de la materia de matemática
- Lápiz
- Bolígrafos colores “Rojo” y “Azul”
- Regla
- Recursos informáticos
- Computador
- Software Matemático Geogebra
- Carpeta Drive documentos
5. Temporalización
Las e-actividades planteadas se realizarán en el transcurso de la semana del 11 al 20 de diciembre.
6.Evaluación
Tarea 1: Infografía sobre propiedades del Triángulo de Pascal
Foro 1: Utilidad de las propiedades del Triángulo de Pascal
6.Evaluación
Tarea 1: Infografía sobre propiedades del Triángulo de Pascal
Foro 1: Utilidad de las propiedades del Triángulo de Pascal
Tarea 2: Para realizar una aplicación del triángulo de Pascal y sus propiedades; deberás seguir los siguientes pasos:
- Reunirse en equipos de 3 o 4 personas y buscar en Internet páginas o vídeos de donde puedan obtener información para ampliar más el tema del triángulo de Pascal.
- Con la información obtenida, realizar un vídeo donde se expliquen cada uno de los problemas; explicando la fórmula matemática, elementos, características, diseño en Geogebra.
DATOS QUE DEBE CONTENER EL VÍDEO:
· Título del Tema
· Nombre del docente
· Nombres de los integrantes del equipo
· Grupo
· Fecha
3. El objetivo de demostrar o comprobar las propiedades del Triángulo de Pascal mientras se graban en vídeo.
4. Finalmente deben generar una conclusión contestando a la pregunta: ¿Para qué me sirve el Triángulo de Pascal?
5. Deben enviar el URL (link) de sus videos al correo del docente: matematikinteractiva_carlos@hotmail.com
Tarea 3: Aplicación realizada en Geogebra
Compruebe en geogebra las siguientes propiedades:
Nota: Las tareas tendrán una calificación sobre 10, utilizando una rúbrica.
Foros: Idóneo o no idóneo.
Tarea 4: Ingresar al ThatQuiz del siguiente link: https://www.thatquiz.org/es/practicetest?iy3qiojzc493
En este link se puede evaluar el contenido que refiere analizar las propiedades del triángulo de Pascal mediante la resolución de problemas.
Como herramienta didáctica adicional tenemos a Geogebra que es un programa dinámico para la Enseñanza y Aprendizaje de las matemáticas para educación en todos sus niveles.
Combina dinámicamente, geometría, álgebra , análisis y estadística en un único conjunto tan sencillo a nivel operativo.
Este programa les facilitara la evaluación ya que permite abordar la geometría desde una forma dinámica e interactiva que ayuda a los estudiantes a visualizar contenidos matemáticos que son más complicados de afrontar desde un dibujo estático.
También permite realizar construcciones de manera fácil y rápida, con un trazado exacto y real, que además, revelarán las relaciones existentes entre la figura construida; también permitirá la transformación dinámica de los objetos que la componen.
Debido a estas dos características el profesorado y el alumnado pueden acercarse a GeoGebra de varias maneras, no excluyentes entre sí pero que a menudo están relacionadas con el nivel de capacitación que se tenga del programa.


No hay comentarios:
Publicar un comentario